Writeup Midnight Flag 2023 - AnotherCrackMe

Writeup Midnight Flag CTF 2023 - AnotherCrackMe

Description:

Un vendeur de protection de logiciels embarqués nous a mis au défi de lui prouver que cette technologie est inefficace.

Dans le cas contraire, toutes les technologies qui seront embarquées sur le nouvel avion de LockFeet Martine seront protégées par cette technologie.

Fichier : https://cdn.midnightflag.fr/AnotherCrackMe

Auteur : deadc0de

A vendor of embedded software protection challenged us to prove to him that this technology is ineffective.

Otherwise, all the technologies that will be embarked on the new aircraft of LockFeet Martine will be protected with this technology.

File : https://cdn.midnightflag.fr/AnotherCrackMe

Author: deadc0de

Files:

AnotherCrackMe

🧼 Recon and cleaning

Let's start with some understanding of what we got here.

$ file AnotherCrackMe
AnotherCrackMe: Mach-O 64-bit arm64 executable, flags:<NOUNDEFS|DYLDLINK|TWOLEVEL|WEAK_DEFINES|BINDS_TO_WEAK|PIE>

Ok, so it seems we have to deal with an ARM Mac OS executable. I can guess the challenge author did not want us to do some dynamic debugging. Let's open it in Ghidra.

It automatically detect it as an AARCH64 Mach-O binary.

At the entry point, we directly have the challenge code, which is comparing each character of our input one by one. The first checks are:

As you can see, the Ghidra decompiler has a hard time detecting that our input is an array of characters. Since the first if is checking strlen(input) == 26, we can assume the array is at least 26 characters long and clean up the decompilation so it looks better. The following gif shows my whole cleaning process.

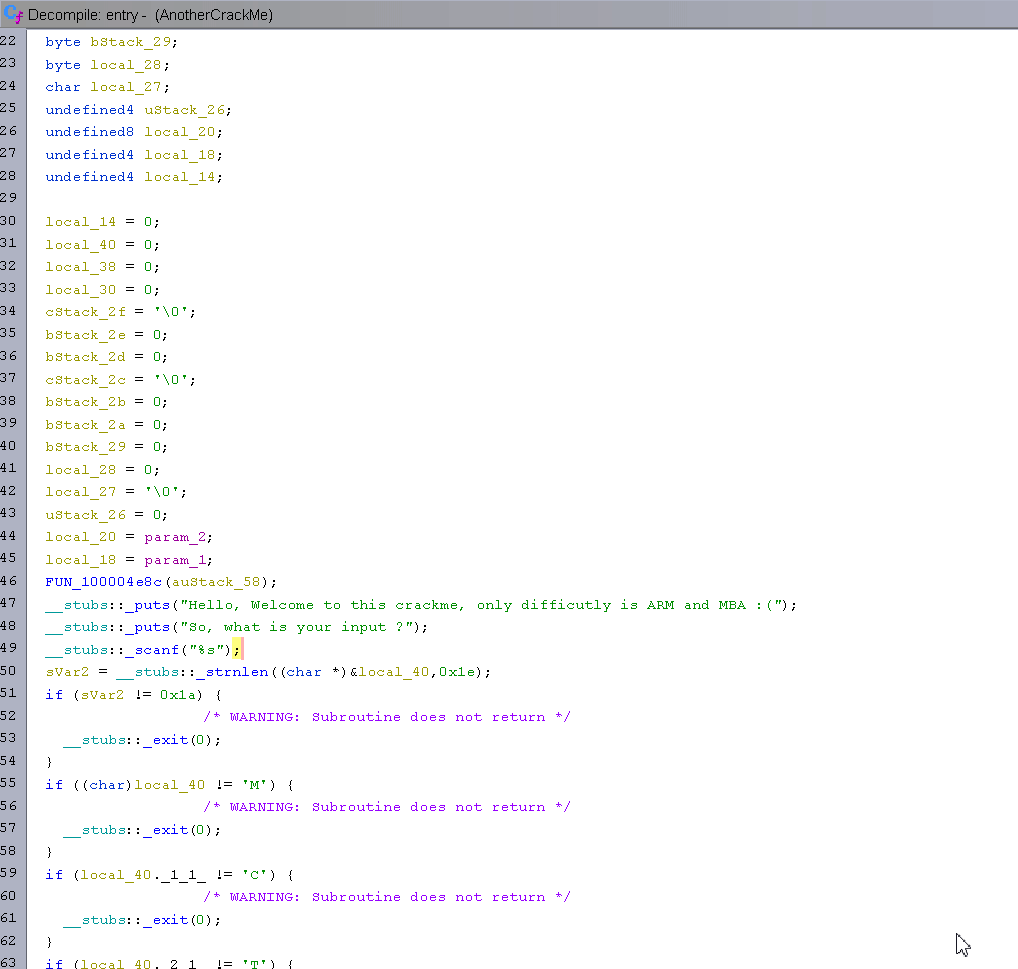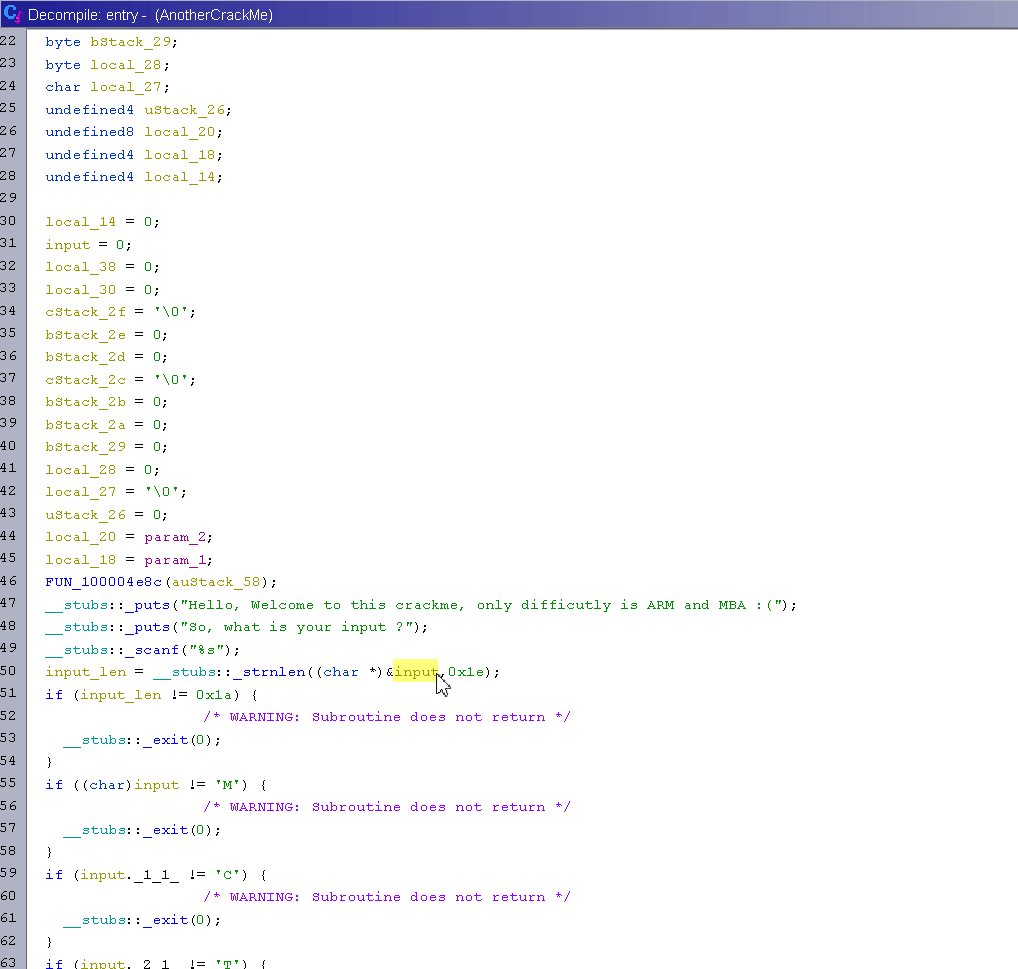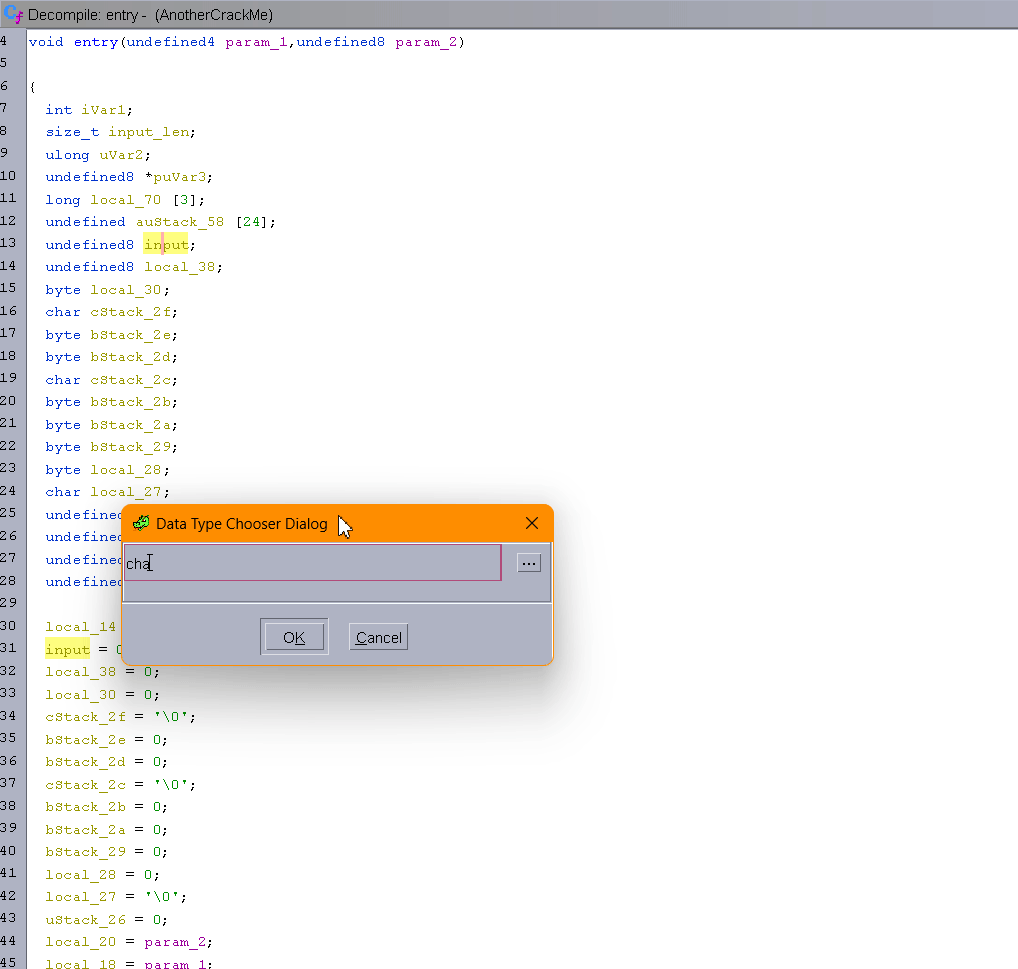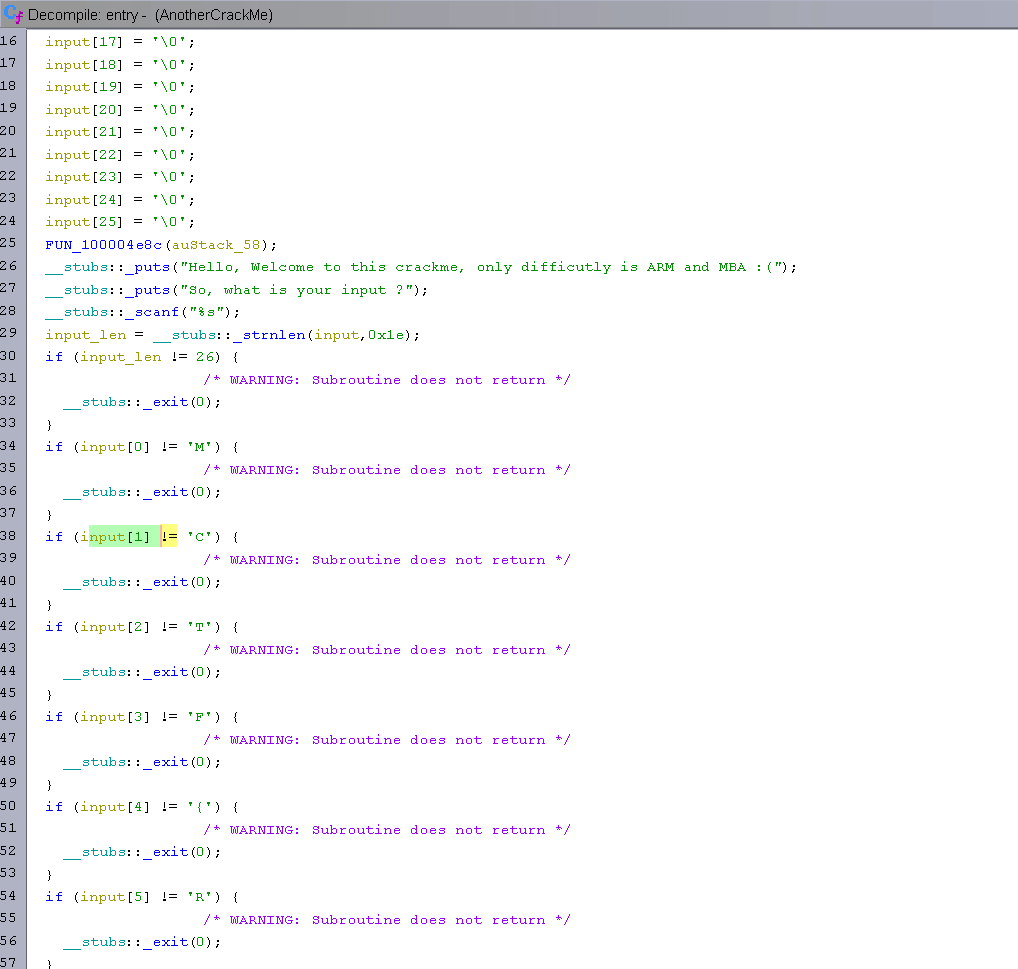
Now that Ghidra is showing the good indexes that are used, this will ease a lot of the reversing process.

📟 Reversing the binary

The first comparisons are straight forward, as you can see in the most basic crackmes.

It starts to get a little fishy around character 12:

And we have the following messages spread around the different comparisons:

Gota say that expression starts to get difficult, dont you think ?
What if i've tried to STOP symexec abuser but it didn't work ? :)

Surely the architecture has been chosen so we can't use tools like angr to dynamically bruteforce the flag. There is also a pitfall made to break such a technique:

__stubs::_puts("Sorry, so here is a vector ");
while (uVar2 = FUN_100004eb8(auStack_58), uVar2 < 2500000)
{
    iVar1 = FUN_1000043b8(0,0x1e);
    local_70[0] = (long)input[iVar1];
    FUN_100004ee0(auStack_58,local_70);
}

As I don't have the time nor the patience to solve all those equations by hand, I will use the z3 solver!

⌨️ Z3 to the rescue

I have heard a lot about z3, but this is actually the first time that I'm using it.

Basicaly, z3 is a theorem prover used to solve arithmetic problems or equations. Let's take a little example. If we want to solve the equation x * 4 == 16, we will do the following in python:

>>> from z3 import *
>>> x = Int("x")
>>> solve(x * 4 == 16)
[x = 4]

Quite easy, right? This way of doing things is not very efficient because we can't get the result and process it afterward. We will use the Solver object instead.

This is the same example, but by using the Solver object:

>>> s = Solver()
>>> x = Int("x")
>>> s.add(x * 4 == 16)
>>> s.check() # check if it can found a result to our equation
sat
>>> sol = s.model() # get a solution of the equation
>>> print(sol)
[x = 4]
>>> print(sol[x])
4 # there is it!

📄 Script and final thoughts

Now, I have everything I need to know to start writing my final script.

The final script goes as follows:

from z3 import *

def solve_print(e, s, x):
    s.push()
    s.add(e)
    s.check()
    # Get the result and show its character representation
    print(chr(int(str(s.model()[x]))), end="")
    s.pop()

if __name__ == "__main__":

    s = Solver()
    x = BitVec('x', 8)

    print("MCTF{R3v3rs", end="")

    solve_print(((~((~x ^ 0xffffffff) & 0x12) & ((x ^ 0xffffffff) & 0xffffffed ^ 0xffffffff)) == 0x21), s, x)

    print("_", end="")

    #solve_print((((x ^ 0xffffffff | 0x14) + (x ^ 0xffffffff | 0x14)) - ~x == 0x73), s, x)

    solve_print(((~((~x & (x ^ 0xffffffff)) + 0x20) & ((~x & (x ^ 0xffffffff)) + 0x20 ^ 0xffffffff)) == 0x29), s, x)

    solve_print((((x | 0xf) + (~x | 0xf)) - ~x == 0x44), s, x)

    print("_", end="")

    solve_print((((~(x & 7) & (~x & 0xfffffff8 ^ 0xffffffff) | 0xf) + (~(~(x & 7) & (~x & 0xfffffff8 ^ 0xffffffff)) | 0xf)) - ~(~(x & 7) & (~x & 0xfffffff8 ^ 0xffffffff)) == 0x43), s, x)

    print("4", end="")

    solve_print(((~((~x ^ 0xffffffff) & 0x41) & ((x ^ 0xffffffff) & 0xffffffbe ^ 0xffffffff)) == 0x1b), s, x)

    solve_print((((~(~((~x & (x ^ 0xffffffff)) + 0x2d) & ((~x & (x ^ 0xffffffff)) + 0x2d ^ 0xffffffff)) ^ 0xffffffff | 100) + (~((~x & (x ^ 0xffffffff)) + 0x2d) & ((~x & (x ^ 0xffffffff)) + 0x2d ^ 0xffffffff) ^ 0xffffffff | 100)) - ~(~((~x & (x ^ 0xffffffff)) + 0x2d) & ((~x & (x ^ 0xffffffff)) + 0x2d ^ 0xffffffff)) == 0xb0), s, x)

    print("_", end="")

    solve_print(((((x ^ 0x12) + (x & 0x12) * 2) * 0x27 + 0x17) * 0x97 == 0x8adf1), s, x)

    solve_print(((~((~x ^ 0xffffffff) & 0xbaba) & ((x ^ 0xffffffff) & 0xffff4545 ^ 0xffffffff)) == 0xba8e), s, x)

    solve_print(((x & 0xf1 | ~x & 0xe) == 0x66), s, x)

    solve_print((((((x ^ 0x92) + (x & 0x92) * 2) * 0x27 + 0x17) * 0x97 == 0x12d562)), s, x)

    print("}")

Flag: MCTF{R3v3rs3_I5_34Zy_N4h?}

Thanks a lot for reading until here! I hope I have demistified a bit z3 if you didn't know about it, it's such a great tool that can make you save a lot of time when reversing complex arithmetic operations.

Author: Ooggle